Mathematical Set Up

Suppose we have a training matrix X with n observations and d features X=(x11x12…x1dx21x22…x2d⋮⋮⋱⋮xn1xn2…xnd)=(x⊤1x⊤2⋮x⊤n)∈Rn×d

and that we want to do a feature transform of this data using the Radial Basis Function. To do this, we

  • choose b rows of X and we call them centroids x(1),…,x(b)
  • calculate using some heuristic a bandwidth parameter σ2

And then, for every centroid we define a radial basis function as follows ϕ(i)(x):=exp(−∥x−x(i)∥2σ2)∀i∈{1,…,b}for x∈Rd

We can therefore obtain a transformed data matrix as Φ:=(1ϕ(1)(x1)ϕ(2)(x1)⋯ϕ(b)(x1)1ϕ(1)(x2)ϕ(2)(x2)⋯ϕ(b)(x2)⋮⋮⋮⋱⋮1ϕ(1)(xn)ϕ(2)(xn)⋯ϕ(b)(xn))∈Rn×(b+1)
 Then we fit a regularized linear model so that optimal parameters are given by w:=(Φ⊤Φ+λIn)−1Φ⊤y
 These parameters are usually found by solving the associated system of linear equations for w (Φ⊤Φ+λIn)w=Φ⊤y
 This will be one of the strategies that we’ll see below. However, we are required to apply regularization with a very small regularization parameter λ. This hints at the fact that maybe we can simply set λ=0 and then find w simply by finding the pseudoinverse of Φ (Φ⊤Φ)−1Φ⊤
 and then multiply this by y on the left. This approach looks more stable and can be implemented by setting pseudoinverse=TRUE in the function make_predictor defined in this document.

Parameters

In the following code chunk you can set up n the number of training observations, d the dimensionality of the input (i.e. the number of features), λ the regularization coefficient, m the number of testing observations, and b dimensionality of the data after the feature transform, which in this case corresponds to the number of centroids.

n <-  1000
d <-  2
lambda <-  0.00001
m <-  200
b <-  50

Training and Testing Sets

We work with synthetic data sets. For simplicity, we will generate X uniformly in an interval (which in this case is [−4,4]) and then y will be taken to be a multivariate normal of each row of X. Note that we create a factory of functions to generate multivariate normal closures, yet the same behavior would be achieved writing up a simple function. The factory of functions is defined in order to work with the functional programming paradigm.

# Explanatory variable is uniformly distributed between -4 and 4, then reshaped
X <-  matrix(runif(n*d, min=-4, max=4), nrow=n, ncol=d)
# Factory of multivariate normal distributions
normal_factory <- function(mean_vector, cov_matrix){
  d <- nrow(cov_matrix)
  normal_pdf <- function(x){
    exponent <- -mahalanobis(x, center=mean_vector, cov=cov_matrix) / 2
    return(
      (2*pi)^(-d/2) * det(cov_matrix)^(-1/2) * exp(exponent)
    )
  }
}
# Closure will be our data-generating process for training and test response.
target_normal <- normal_factory(rnorm(d), diag(d))
y <- matrix(apply(X, 1, target_normal))

Similarly, create test data.

Xtest <- matrix(runif(m*d, min=-4, max=4), nrow=m, ncol=d)
ytest <- matrix(apply(Xtest, 1, target_normal))

Feature Transform Implementation

Define a function that, given a training data matrix X, finds the distance matrix containing all the pairwise distances squared, and then return the median of such distances. Essentially, it returns the badwidth squared σ2.

compute_sigmasq <- function(X){
  # Compute distance matrix expanding the norm. Return its median
  Xcross <- tcrossprod(X)
  Xnorms <- matrix(diag(Xcross), nrow(X), nrow(X), byrow=TRUE)
  return(median(Xnorms - 2*Xcross + t(Xnorms)))
}

Define a function that gets b random samples from the rows of an input matrix X, these will be the centroids.

get_centroids <- function(X, n_centroids){
  # Find indeces of centroids
  idx <- sample(1:nrow(X), n_centroids)
  return(X[idx, ])
}

Construct a factory of Radial Basis Functions. The factory constructs an RBF, given a centroid and a σ2.

rbf <- function(centroid, sigmasq){
  rbfdot <- function(x){
    return(
      exp(-sum((x - centroid)^2) / sigmasq)
    )
  }
  return(rbfdot)
}

Finally, we can put all of these functions together to compute Φ and eventually make predictions.

compute_phiX <- function(X, centroids, sigmasq){
  # Create a list of rbfdot functions and apply each of them to every row of X
  phiX <- mapply(
    function(f) apply(X, 1, f), 
    apply(centroids, 1, rbf, sigmasq=sigmasq)
  )
  # Reshape phiX correctly
  phiX <- matrix(phiX, nrow(X), nrow(centroids))
  # Recall we need the first column to contain 1s for the bias
  return(cbind(1, phiX))  # this is a (n, d+1) matrix
}

Prediction

We’re now ready to define a factory of functions that returns prediction functions.

library(corpcor)
make_predictor <- function(X, y, lambda, n_centroids, pseudoinverse=FALSE){
  # Randomly sample centoids
  centroids <- get_centroids(X, n_centroids)
  sigmasq <- compute_sigmasq(X)
  # Get transformed data matrix
  phiX <- compute_phiX(X, centroids, sigmasq)
  # Find optimal parameters
  if (pseudoinverse){
    # This method works best cause it does automatic regularization with SVD
    w <- pseudoinverse(phiX) %*% y
  } else {
    w <- solve(t(phiX)%*%phiX + lambda*diag(n_centroids+1), t(phiX) %*% y)
  }
  # Construct predictor closure for a new batch of testing data Xtest
  predictor <- function(Xtest){
    # Need to transform test data into a phi matrix
    phi_Xtest <- compute_phiX(Xtest, centroids, sigmasq)
    return(phi_Xtest %*% w)
  }
  return(predictor)
}

We can test its effectiveness now. Notice that in general we might need a lot of centroids to make this work.

# Construct prediction functions. One with regularization, other with pseudoinv
predict <- make_predictor(X, y, lambda, n_centroids = b)
pseudo_predict <- make_predictor(X, y, lambda, n_centroids = b, pseudoinverse = TRUE)
# Get predictions
yhat <- predict(Xtest)
yhat_pseudo <- pseudo_predict(Xtest)

Predictions can be assessed by plotting predicted values against the true test values.

library(ggplot2)
# Put data into a dataframe for ggplot2
df <- data.frame(real=ytest, pred=yhat, pseudo_pred=yhat_pseudo)
ggplot(data=df) + 
  geom_point(aes(x=real, y=pred), color="darkblue") + 
  geom_abline(intercept=0, slope=1) + 
  ggtitle(paste("Predictions vs Actual with b =", b)) + 
  theme(
    plot.title = element_text(hjust = 0.5),
    axis.title = element_text(size=15, face="bold"),
    axis.title.y = element_text(angle=0, vjust=0.5)
  ) +
  xlab(expression(y)) + 
  ylab(expression(hat(y))) + 
  coord_fixed()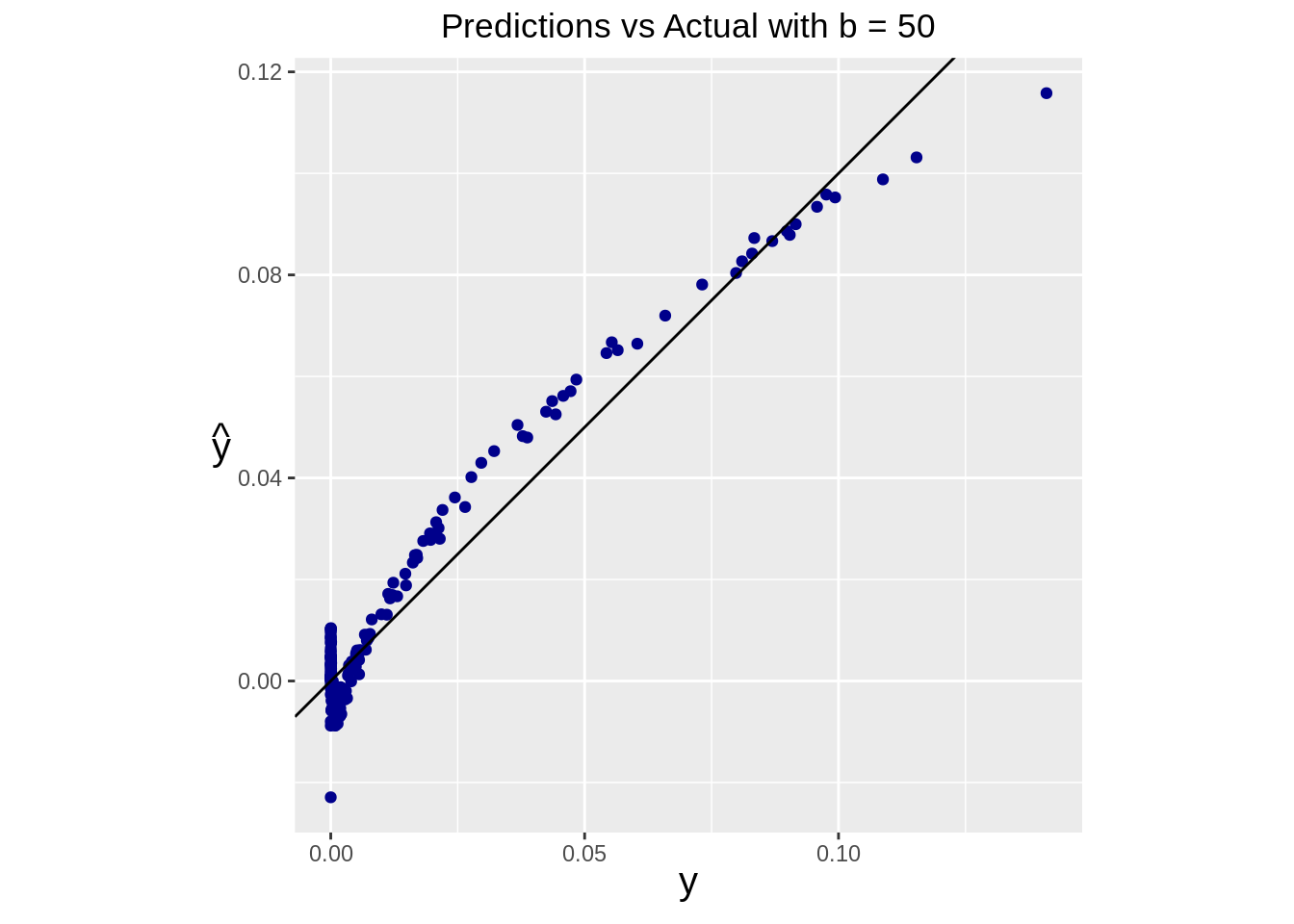

Similarly, we can see the performance of our prediction using the pseudoinverse

ggplot(data=df) + 
  geom_point(aes(x=real, y=pseudo_pred), color="darkblue") + 
  geom_abline(intercept=0, slope=1) + 
  ggtitle(paste("Pseudo-Predictions vs Actual with b =", b)) + 
  theme(
    plot.title = element_text(hjust = 0.5),
    axis.title = element_text(size=15, face="bold"),
    axis.title.y = element_text(angle=0, vjust=0.5)
  ) +
  xlab(expression(y)) + 
  ylab(expression(hat(y))) + 
  coord_fixed()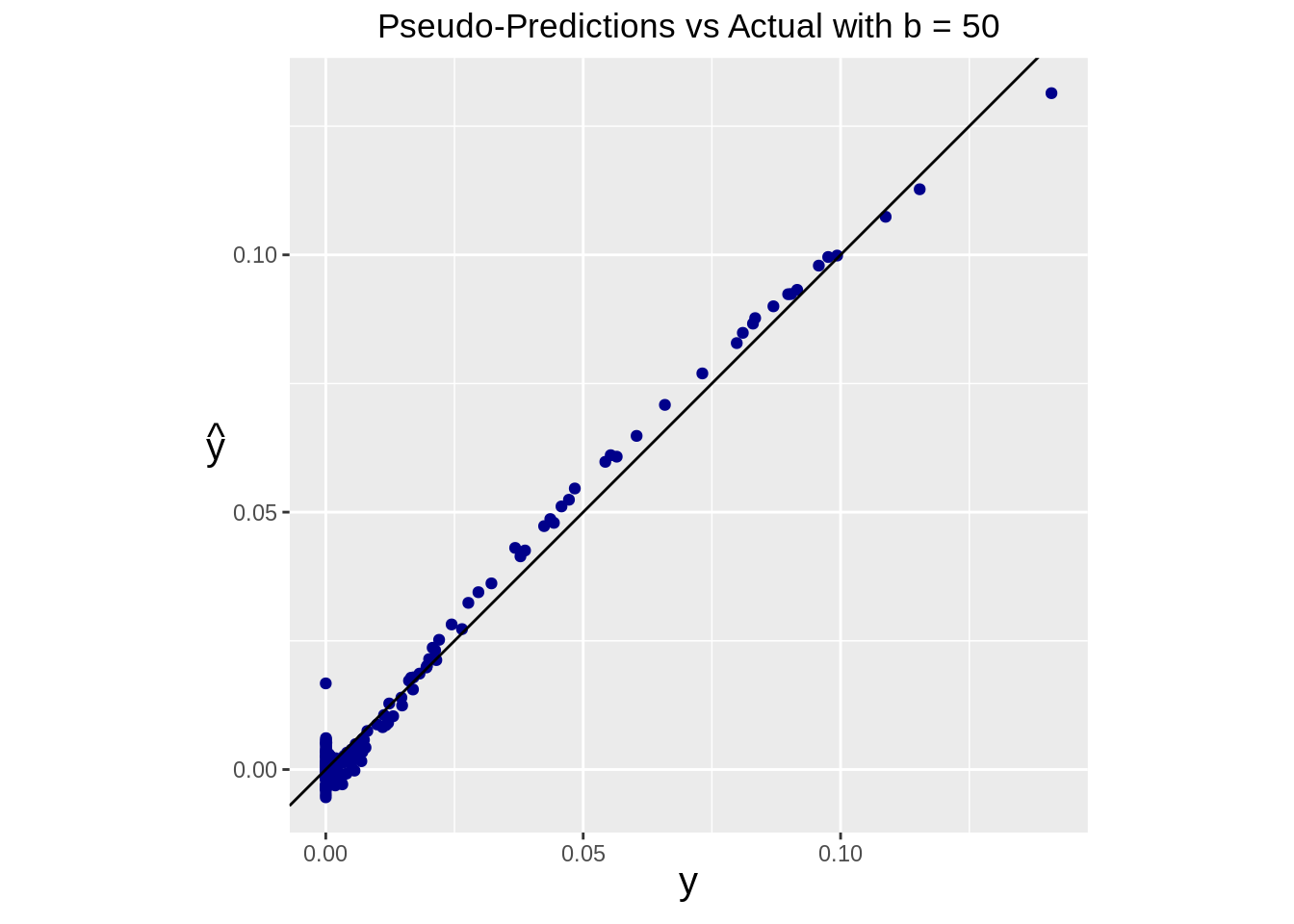

Technical Note on Calculating the Bandwidth

To vectorize this operation, we aim to create a matrix containing all the squared norms of the difference between the vectors D=(∥x1−x1∥2∥x1−x2∥2⋯∥x1−xn∥2∥x2−x1∥2∥x2−x2∥2⋯∥x2−xn∥2⋮⋮⋱⋮∥xn−x1∥2∥xn−x2∥2⋯∥xn−xn∥2)

Notice that we can rewrite the norm of the difference between two vectors xi and xj as follows ∥xi−xj∥2=(xi−xj)⊤(xi−xj)=x⊤ixi−2x⊤ixj+x⊤jxj
 Broadcasting this, we can rewrite the matrix D as D=(x⊤1x1−2x⊤1x1+x⊤1x1x⊤1x1−2x⊤1x2+x⊤2x2⋯x⊤1x1−2x⊤1xn+x⊤nxnx⊤2x2−2x⊤2x1+x⊤1x1x⊤2x2−2x⊤2x2+x⊤2x2⋯x⊤2x2−2x⊤2xn+x⊤nxn⋮⋮⋱⋮x⊤nxn−2x⊤nx1+x⊤1x1x⊤nxn−2x⊤nx2+x⊤2x2⋯x⊤nxn−2x⊤nxn+x⊤nxn)
 This can now be split into three matrices, where we can notice that the third matrix is nothing but the transpose of the first. D=(x⊤1x1x⊤1x1⋯x⊤1x1x⊤2x2x⊤2x2⋯x⊤2x2⋮⋮⋱⋮x⊤nxnx⊤nxn⋯x⊤nxn)−2(x⊤1x1x⊤1x2⋯x⊤1xnx⊤2x1x⊤2x2⋯x⊤2xn⋮⋮⋱⋮x⊤nx1x⊤nx2⋯x⊤nxn)+(x⊤1x1x⊤2x2⋯x⊤nxnx⊤1x1x⊤2x2⋯x⊤nxn⋮⋮⋱⋮x⊤1x1x⊤2x2⋯x⊤nxn)

The key is not to notice that we can obtain the middle matrix from X with a simple operation: XX⊤=(x⊤1x⊤2⋮x⊤n)(x1x2⋯xn)=(x⊤1x1x⊤1x2⋯x⊤1xnx⊤2x1x⊤2x2⋯x⊤2xn⋮⋮⋱⋮x⊤nx1x⊤nx2⋯x⊤nxn)

and then the first matrix can be obtained as follows (11⋮1)n×1(x⊤1x1x⊤2x2⋯x⊤nxn)1×n=(x⊤1x1x⊤1x1⋯x⊤1x1x⊤2x2x⊤2x2⋯x⊤2x2⋮⋮⋱⋮x⊤nxnx⊤nxn⋯x⊤nxn)

where diag[(x⊤1x1x⊤1x2⋯x⊤1xnx⊤2x1x⊤2x2⋯x⊤2xn⋮⋮⋱⋮x⊤nx1x⊤nx2⋯x⊤nxn)]=(x⊤1x1x⊤2x2⋯x⊤nxn)1×n