Profiling Portfolio
Implementations
Data Generation and Problem Settings
Import the necessary packages. The library provfis is a stochastic profiler and can be used to profile our code.
library(profvis)
library(tidyverse)
library(MASS)
library(microbenchmark)First, let’s decide some parameters and settings such as the amount of training and testing data.
Number of data points for plotting & Bandwidth squared of the RBF kernel
ntest <- 500
Characteristic Length-scale for kernel
sigmasq <- 1.0
Number of training points, standard deviation of additive noise
ntrain <- 10
sigma_n <- 0.5
Define number of samples for prior gp mvn and posterior gp mvn to take
nprior_samples <- 5
npost_samples <- 5Define some helper functions. In particular, the kernel function is a squared exponential. The bandwidth is computed as the median of all pairwise distances. We also define a matrix that applies the squared exponential to rows of two matrices, i.e. it computes the kernel matrix \(K(X, Y)\). for two matrices \(X\) and \(Y\). Finally, we also have a regression function which represents the true structure of the data. This is just a quintic polynomial for simplicity, but can be replaced by more complicated functions.
squared_exponential <- function(x, c, sigmasq){
return(exp(-0.5*sum((x - c)^2) / sigmasq))
}
kernel_matrix <- function(X, Xstar, sigmasq){
# compute the kernel matrix
K <- apply(
X=Xstar,
MARGIN=1,
FUN=function(xstar_row) apply(
X=X,
MARGIN=1,
FUN=squared_exponential,
xstar_row,
sigmasq
)
)
return(K)
}
regression_function <- function(x){
val <- (x+5)*(x+2)*(x)*(x-4)*(x-3)/10 + 2
return(val)
}Now let’s actually generate some data
set.seed(12345)
# training data
xtrain <- matrix(runif(ntrain, min=-5, max=5))
ytrain <- regression_function(xtrain) + matrix(rnorm(ntrain, sd=sigma_n))
# testing data
xtest <- matrix(seq(-5,5, len=ntest))Naive Vectorized Implementation
The first implementation that we look at is naive in the sense that it basically blindly copies the operations. This means that we invert \(K + \sigma_n^2 I\) directly.
source("gp_naive.R", keep.source = TRUE)
profvis(result <- gp_naive(xtrain, ytrain, xtest, sigma_n, sigmasq))Online Non-Vectorized Cholesky Implementation
This implementation can also be used online. It is recommended in the “Gaussian Processes for Machine Learning” book.
source("gp_online.R", keep.source = TRUE)
profvis(result_online <- gp_online(xtrain, ytrain, xtest, sigma_n, sigmasq))Online Vectorized-Kernel Cholesky Implementation
We can see that most of the time is spent computing the kernel matrix. We can therefore find a faster way to compute it as follows
kernel_matrix_vectorized <- function(X, sigmasq, Y=NULL){
if (is.null(Y)){
Y <- X
}
n <- nrow(X)
m <- nrow(Y)
# Find three matrices above
Xnorm <- matrix(apply(X^2, 1, sum), n, m)
Ynorm <- matrix(apply(Y^2, 1, sum), n, m, byrow=TRUE)
XY <- tcrossprod(X, Y)
return(exp(-(Xnorm - 2*XY + Ynorm) / (2*sigmasq)))
}using this, we get
source("gp_online_vect.R", keep.source = TRUE)
profvis(gp_online_vect(xtrain, ytrain, xtest, sigma_n, sigmasq))We can see that this implementation uses much less memory and it’s much faster.
Completely vectorized implementation
We can combine these ideas to obtain a much faster implementation.
source("gp_completely_vectorized.R", keep.source = TRUE)
profvis(gp_completely_vectorized(xtrain, ytrain, xtest, sigma_n, sigmasq), interval=0.005)Visualizations
Before seeing training data
Before seeing the training data we only have the test data. The Gaussian Process will therefore predict random (smooth) functions with mean zero.
Kss <- kernel_matrix_vectorized(xtest, sigmasq)
# Sample nprior_samples Multivariate Normals with mean zero and variance-covariance
# being the kernel matrix
data.frame(x=xtest, t(mvrnorm(nprior_samples, rep(0, length=ntest), Kss))) %>%
setNames(c("x", sprintf("Sample %s", 1:nprior_samples))) %>%
gather("MVN Samples", "Value", -x) %>%
ggplot(aes(x=x, y=Value)) +
# Because diag(Kss) are all 1s. We use mean +\- 2*standard deviation
geom_rect(xmin=-Inf, xmax=Inf, ymin=-2, ymax=2, fill="grey80") +
geom_line(aes(color=`MVN Samples`)) +
geom_abline(slope=0.0, intercept=0.0, lty=2) +
scale_y_continuous(lim=c(-3, 3)) +
labs(title=paste(nprior_samples, "MVN Samples before seeing the data")) +
theme(plot.title=element_text(hjust=0.5))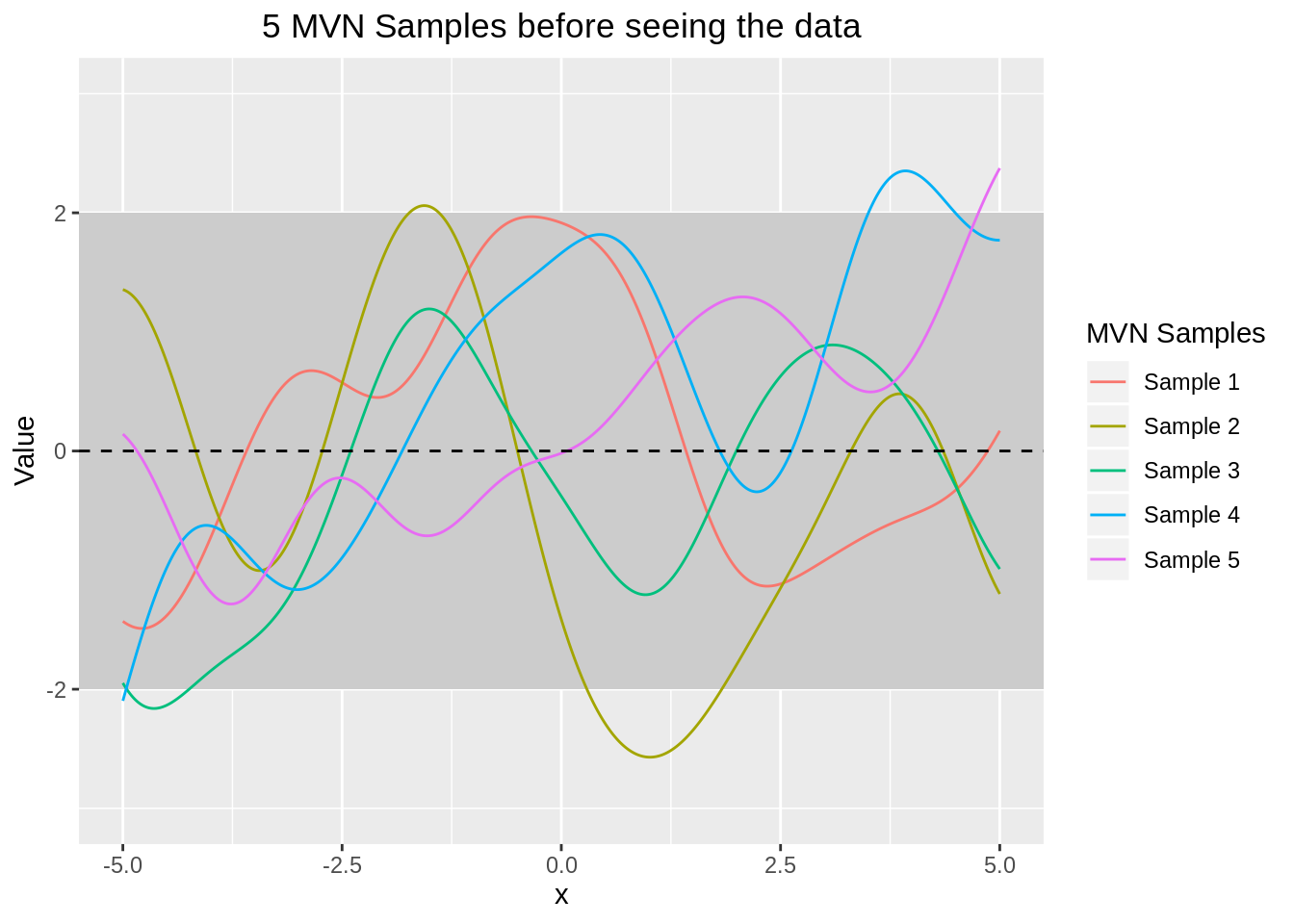
After seeing training data
We only need to find the predicted mean and the predicted variance.
# Get predicitons. To predict noisy data just add sigma_n^2*diag(ncol(xtest))
# to the covariance matrix as implemented in the script
results <- gp_completely_vectorized(xtrain, ytrain, xtest, sigma_n, sigmasq)
gpmean <- results[[1]]
gpvcov <- results[[2]]
# for plotting
dftrain = data.frame(xtrain=xtrain, ytrain=ytrain)
# Plot
data.frame(x=xtest, t(mvrnorm(npost_samples, gpmean, gpvcov))) %>%
setNames(c("x", sprintf("Sample %s", 1:npost_samples))) %>%
mutate(ymin=gpmean-2*sqrt(diag(gpvcov)), ymax=gpmean+2*sqrt(diag(gpvcov)),
gpmean=gpmean, ytrue=regression_function(xtest)) %>%
gather("MVN Samples", "Value", -x, -ymin, -ymax, -gpmean, -ytrue) %>%
ggplot(aes(x=x, y=Value)) +
geom_ribbon(aes(ymin=ymin, ymax=ymax), fill="grey80") +
geom_line(aes(color=`MVN Samples`)) +
geom_line(aes(y=gpmean), size=1) +
geom_line(aes(y=ytrue), color="darkred", lty=2) +
geom_point(data=dftrain, aes(x=xtrain, y=ytrain), color="red") +
ggtitle(paste(npost_samples, "MVN Samples after seeing", ntrain, "data points")) +
theme(plot.title=element_text(hjust=0.5))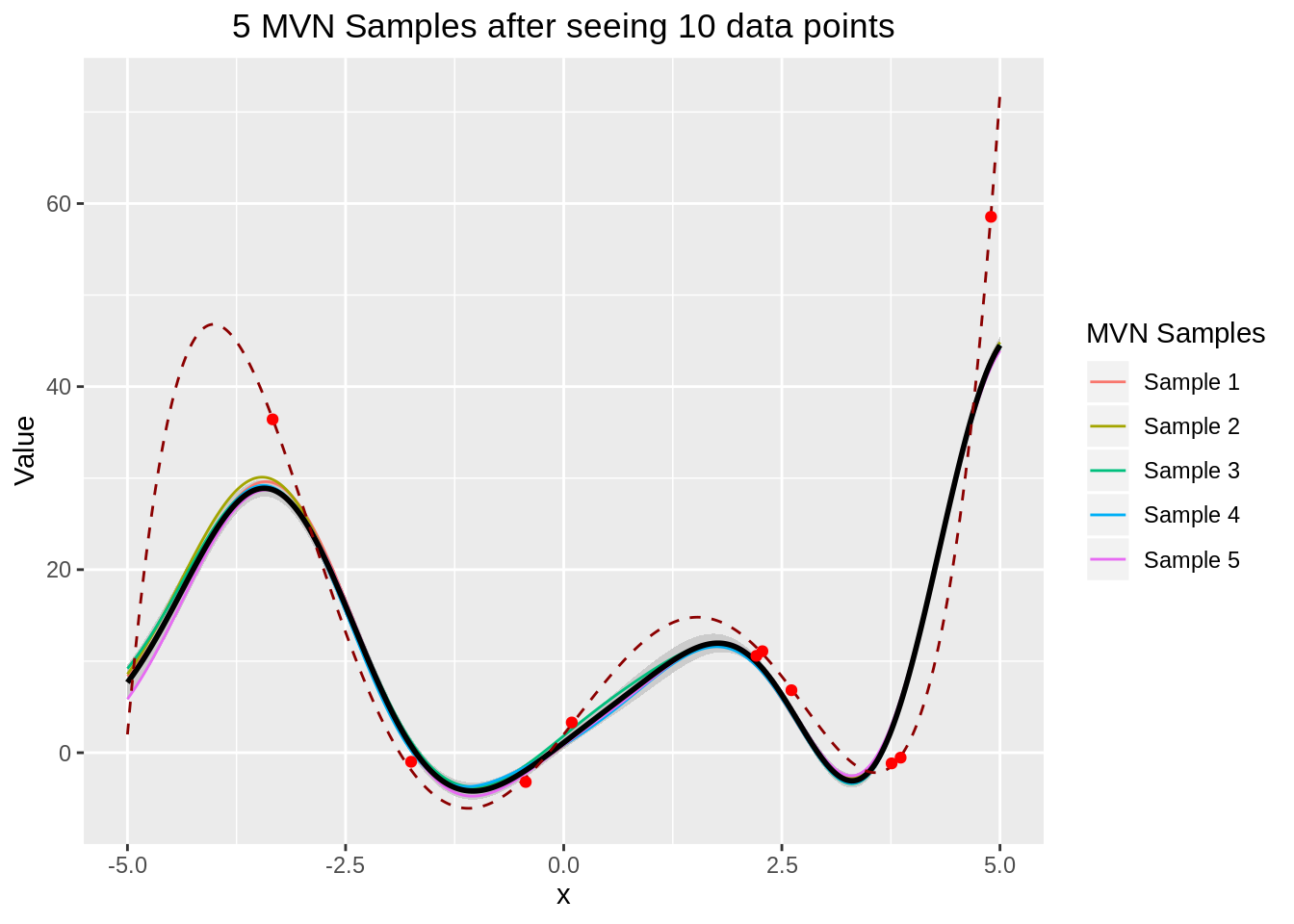
Note on Vectorized Kernel Matrix
One might wonder why in the function kernel_matrix_vectorized() we fill the matrix Ynorm by row. Afterall R works with column-major storage so this should be inefficient. One can compare filling in a matrix by row versus filling it by column and then taking the transpose in different cases:
- Number of rows < Number of columns
nrows <- 100
ncols <- 2000
microbenchmark(
rowwise=matrix(0, nrows, ncols, byrow=TRUE),
transpose=t(matrix(0, nrows, ncols))
)## Unit: microseconds
## expr min lq mean median uq max neval
## rowwise 321.202 343.0085 648.0742 360.0345 697.1185 5734.401 100
## transpose 534.310 569.7350 950.3921 608.9455 1233.3545 3354.230 100- Number of rows = Number of columns
nrows <- 2000
ncols <- 2000
microbenchmark(
rowwise=matrix(0, nrows, ncols, byrow=TRUE),
transpose=t(matrix(0, nrows, ncols))
)## Unit: milliseconds
## expr min lq mean median uq max neval
## rowwise 16.69890 24.08596 26.52232 24.48049 28.26676 91.81093 100
## transpose 23.32213 29.73081 38.70225 36.65087 41.26867 96.43356 100- Number of rows > Number of columns
nrows <- 2000
ncols <- 100
microbenchmark(
rowwise=matrix(0, nrows, ncols, byrow=TRUE),
transpose=t(matrix(0, nrows, ncols))
)## Unit: microseconds
## expr min lq mean median uq max neval
## rowwise 378.090 383.898 470.1237 392.2410 398.4715 2512.430 100
## transpose 564.521 579.105 688.0039 593.8405 621.8380 2687.371 100Generally, byrow=TRUE is faster.
